Week 13: First-Order Circuits

First-Order Circuits

What are First-Order Circuits?

First order circuits are circuits that contain only one energy storage element (capacitor or inductor), and that can, therefore, be described using only a first order differential equation. The two possible types of first-order circuits are:

1. RC (resistor and capacitor)
2. RL (resistor and inductor)

RL and RC circuits is a term we will be using to describe a circuit that has either a) resistors and inductors (RL), or b) resistors and capacitors (RC).

(A).

An RL Parallel Circuit:

An RL Circuit has at least one resistor (R) and one inductor (L). These can be arranged in parallel, or in series. Inductors are best solved by considering the current flowing through the inductor. Therefore, we will combine the resistive element and the source into a Norton Source Circuit. The Inductor then, will be the external load to the circuit. We remember the equation for the inductor:

V(t) = L(di/dt)

If we apply KCL on the node that forms the positive terminal of the voltage source, we can solve to get the following differential equation:

I_source(t) = Ldi_inductor(t)/R_ndt + I_inductor(t)

The "Source-Free" RL Circuit:

If we take our previous circuit, wait for a while for the current to level off, and then open the switch so the battery is no longer in the circuit, what happens. If the circuit had just a resistor the current would drop immediately to zero. With the inductor the change in current means a change in magnetic flux so the inductor opposes the change. The current does eventually reach zero but it takes some time to get there.

To see why, apply Kirchoff's loop rule. With the switch opened we have:

IR + L dI/dt = 0

or dI/dt = -IR/L

Solving this for current gives I(t) = I_o e^-t/t

The potential difference across the resistor has a similar form:

DV_R = e e^-t/t

The potential difference across the inductor is negative because it's acting like a battery hooked up in the opposite direction:

DV_L = -e e^-t/t

Once again, the graph of current as a function of time in the RL circuit has the same form as the graph of the capacitor voltage as a function of time in the discharging RC circuit, while the graph of the inductor voltage as a function of time in the RL circuit has the same form as the graph of current vs. time in the discharging RC circuit.

Graph:

(B).

An RC Parallel Circuit:

An RC circuit is a circuit that has both a resistor (R) and a capacitor (C). Like the RL Circuit, we will combine the resistor and the source on one side of the circuit, and combine them into a thevenin source. Then if we apply KVL around the resulting loop, we get the following equation:

V_source = RC( dv_capacitor(t)/dt) + V_capacitor (t)

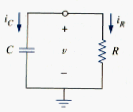
The "Source-Free" RC Circuit

When applied, 

dV_C/dt + dV_R/dt = 0,

where V_C is the voltage drop across the capacitor and V_R is the voltage drop across the resistor.

The change in the voltage drop across the capacitor is given by our previous expression,

dV_C/dt = 1/C

The change in the voltage drop across the resistor can be obtained from Ohm's law

V_R=RI=dV_R/dt=Rdi/dt

Substituting these changes in voltage into Kirchoff's equation gives

1/C + Rdi/dt = 0,

where the current due to the flow of charge on or off the capacitor is the same as through the resistor.

Now we need some initial conditions. Notice that although the capacitor behaves as an open circuit to DC, current must flow to charge or discharge the capacitor. Lets take the case where the capacitor is initially charged and then the circuit is closed and the charge is allowed to drain off the capacitor (eg. closing a switch). The resulting current will flow through the resistor.

Solving for the current we obtain

I(t) = I₀e ^t/RC

where V(T=0) = V_O is the initial voltage across the capacitor and t=RC is the commonly defined time constant of the decay. You should also be able to solve for the voltage across the capacitor and charge on the capacitor.

For the case of an applying voltage V_R being suddenly placed into the circuit (inserting a battery) the capacitor is initially not charged and the voltage across the capacitor is

Graph:

Reflection:

There are two types of First-Order Circuits, These are the Resistor-Inductor circuits or RL and the Resistor-Capacitor circuits or RC. First-Order circuits are characterized by a First-Order differential equation. There are also "Source-Free" RL and RC circuits. The sources in these circuits are usually separated from a switch and when the switch is turned on, the switch will supply power to the capacitor or inductor and when the switch is turned off, there is still power in the circuit because the capacitor and inductors absored energy from the source. 

Video(s):

RL Circuit

RC Circuit

Source-Free RC circuits

When you look at the inner workings of electrical things, you see wires. Until the current passes through them, there will be no light. That wire is you and me. The current is God. We have the power to let the current pass through us, use us, to produce the light of the world, Jesus, in us. Or we can refuse to be used and allow darkness to spread.

--Mother Teresa

Week 12 (Part 2): Capacitors and Inductors

Capacitors 

What are Capacitors?

- In a way, a capacitor is a little like a battery. Although they work in completely different ways, capacitors and batteries both store electrical energy. If you have read know how batteries work, then you know that a battery has two terminals. Inside the battery, chemical reactions produce electrons on one terminal and absorb electrons on the other terminal. A capacitor is much simpler than a battery, as it can't produce new electrons -- it only stores them.

In this section, we'll learn exactly what a capacitor is, what it does and how it's used in electronics. We'll also look at the history of the capacitor and how several people helped shape its progress.

Inside the capacitor, the terminals connect to two metal plates separated by a non-conducting substance, or dielectric. 

In theory, the dielectric can be any non-conductive substance. However, for practical applications, specific materials are used that best suit the capacitor's function. Mica, ceramic, cellulose, porcelain, Mylar, Teflon and even air are some of the non-conductive materials used. The dielectric dictates what kind of capacitor it is and for what it is best suited. Depending on the size and type of dielectric, some capacitors are better for high frequency uses, while some are better for high voltage applications. Capacitors can be manufactured to serve any purpose, from the smallest plastic capacitor in your calculator, to an ultra capacitor that can power a commuter bus. NASA uses glass capacitors to help wake up the space shuttle's circuitry and help deploy space probes. 

Capacitor Circuit

In an electronic circuit, a capacitor is shown like this:

When you connect a capacitor to a battery, here's what happens:

• The plate on the capacitor that attaches to the negative terminal of the battery accepts electrons that the battery is producing.
• The plate on the capacitor that attaches to the positive terminal of the battery loses electrons to the battery.

Once it's charged, the capacitor has the same voltage as the battery (1.5 volts on the battery means 1.5 volts on the capacitor). For a small capacitor, the capacity is small. But large capacitors can hold quite a bit of charge. You can find capacitors as big as soda cans that hold enough charge to light a flashlight bulb for a minute or more.

Let's say you hook up a capacitor like this:

Here you have a battery, a light bulb and a capacitor. If the capacitor is pretty big, what you will notice is that, when you connect the battery, the light bulb will light up as current flows from the battery to the capacitor to charge it up. The bulb will get progressively dimmer and finally go out once the capacitor reaches its capacity. If you then remove the battery and replace it with a wire, current will flow from one plate of the capacitor to the other. The bulb will light initially and then dim as the capacitor discharges, until it is completely out.

Capacitors in Series Connection:

To calculate the total overall capacitance of two capacitors connected in this way you can use the following formula:

1/C_Total = 1/C₁ + 1/C₂ + 1/C_n ….

Example: To calculate the total capacitance for these two capacitors in series.

Capacitors in Parallel Connection:

To calculate the total overall capacitance of two capacitors connected in this way you can use the following formula:

C_Total = C₁ + C₂ + C_n …..

Example: Calculate the total capacitance of these capacitors in parallel.

C_Total = C₁ + C₂ + C₃

= 0.1uF + 0.2uF + 0.3uF

= 0.6uF

Voltage - Current relationship of a capacitor

     

There is a relationship between the charge on a capacitor and the voltage across the capacitor.  The relationship is simple. For most dielectric/insulating materials, charge and voltage are linearly related.

Q = C V

where:

• V is the voltage across the plates.

You will need to define a polarity for that voltage. We've defined the voltage above. You could reverse the "+" and "-".

• Q is the charge on the plate with the "+" on the voltage polarity definition.
• C is a constant - the capacitance of the capacitor.

        The relationship between the charge on a capacitor and the voltage across the capacitor is linear with a constant, C, called the capacitance.

Q = C V

        When V is measured in volts, and Q is measured in coulombs, then C has the units of farads. Farads are really coulombs/volt.

Because dq(t)/dt is the current through the capacitor, you get the following i-v relationship:

To express the voltage across the capacitor in terms of the current, you integrate the preceding equation as follows:

The second term in this equation is the initial voltage across the capacitor at time t = 0.

Energy stored in a capacitor

The energy stored on a capacitor can be calculated from the equivalent expressions:

Inductors

What are Inductors?

-An inductor, also called a coil or reactor, is a passive two-terminal electrical component which resists changes in electric current passing through it. It consists of a conductor such as a wire, usually wound into a coil. When a current flows through it, energy is stored temporarily in a magnetic field in the coil. When the current flowing through an inductor changes, the time-varying magnetic field induces a voltage in the conductor, according to Faraday’s law of electromagnetic induction, which opposes the change in current that created it.

An inductor is characterized by its inductance, the ratio of the voltage to the rate of change of current, which has units of henries (H). Inductors have values that typically range from 1 µH (10⁻⁶H) to 1 H. Many inductors have a magnetic core made of iron or ferrite inside the coil, which serves to increase the magnetic field and thus the inductance. Along with capacitors and resistors, inductors are one of the three passive linear circuit elements that make up electric circuits. Inductors are widely used in alternating current (AC) electronic equipment, particularly in radio equipment. They are used to block the flow of AC current while allowing DC to pass; inductors designed for this purpose are called chokes. They are also used in electronic filters to separate signals of different frequencies, and in combination with capacitors to make tuned circuits, used to tune radio and TV receivers.

Inductors in Series Connection

Thus, the total inductance for series inductors is more than any one of the individual inductors' inductances. The formula for calculating the series total inductance is the same form as for calculating series resistances:

Inductors in Parallel Connection

Thus, the total inductance is less than any one of the individual inductors' inductances. The formula for calculating the parallel total inductance is the same form as for calculating parallel resistances:

Voltage - Current relationship of an inductor

Here’s the defining equation for the inductor:

where the inductance L is a constant measured in henries (H). Here is the same equation in graphical form.

To express the current through the inductor in terms of the voltage, you integrate the preceding equation as follows:

Energy stored in an Inductor

The energy equation implies that the energy in the inductor is always positive. The inductor absorbs power from a circuit when storing energy, and the inductor releases the stored energy when delivering energy to the circuit.

Reflection
This week, we also discussed Capacitors and Inductors together with Maximum Power Transfer. Capacitors and Inductors are passive elements in a circuit, meaning that they cannot generate energy, they drop it instead. Capacitors are components that store electrical energy and when the capacitor is full of electrical energy, it is in a "charged" state. To discharge a capacitor, you need to connect a resistor in both of its terminals. Capacitors are made up of two metal plates and separated by a non-conducting substance or dielectric. Capacitors are also measured in farads but most of the time, You'll only find capacitors in micro farads (F) because one farad is a pretty huge number. Inductors are basically just coils of conducting wires and they are measured in henries (H). Like the capacitor, it also stores electrical energy but it stores it in a form of a magnetic field. 

Video(s):
Capacitors

Inductors

“I've found out so much about electricity that I've reached the point where I understand nothing and can explain nothing.

[Describing his experiments with the Leyden jar.]” 

― Pieter van Musschenbroek

Week 12: Maximum Power Transfer

Maximum Power Transfer

What is Maximum Power Transfer?
-In electrical engineering, the maximum power transfer theorem states that, to obtain maximum external power from a source with a finite internal resistance, the resistance of the load must equal the resistance of the source as viewed from its output terminals. Moritz von Jacobi published the maximum power (transfer) theorem around 1840; it is also referred to as "Jacobi's law".

The theorem results in maximum power transfer, and not maximum efficiency. If the resistance of the load is made larger than the resistance of the source, then efficiency is higher, since a higher percentage of the source power is transferred to the load, but the magnitude of the load power is lower since the total circuit resistance goes up.

If the load resistance is smaller than the source resistance, then most of the power ends up being dissipated in the source, and although the total power dissipated is higher, due to a lower total resistance, it turns out that the amount dissipated in the load is reduced.

The theorem states how to choose (so as to maximize power transfer) the load resistance, once the source resistance is given. It is a common misconception to apply the theorem in the opposite scenario. It does not say how to choose the source resistance for a given load resistance. In fact, the source resistance that maximizes power transfer is always zero, regardless of the value of the load resistance.

Procedures in applying Maximum Power Transfer:

·        * Apply Thevenin’s Theorem on a circuit

·        *  Solve for V_Th and R_Th

·        * Apply the power delivered to the load resistance (R_L) and R_L = R_Th, The formula for power delivered to R_L is:

* To find the maximum power, differentiate the above expression with respect to resistance R_L and equate it to zero. Thus,

Thus in this case, the maximum power will be transferred to the load when load resistance is just equal to internal resistance of the battery.

Example:

Find the power dissipated by the 0.8Ω resistor.  

With this value of load resistance, the dissipated power will be 39.2 watts:

If we were to try a lower value for the load resistance (0.5 Ω instead of 0.8 Ω, for example), our power dissipated by the load resistance would decrease:

Power dissipation increased for both the Thevenin resistance and the total circuit, but it decreased for the load resistor. Likewise, if we increase the load resistance (1.1 Ω instead of 0.8 Ω, for example), power dissipation will also be less than it was at 0.8 Ω exactly:

Reflection:

The Maximum Power Transfer Theorem is not so much a means of analysis as it is an aid to system design. Simply stated, the maximum amount of power will be dissipated by a load resistance when that load resistance is equal to the Thevenin/Norton resistance of the network supplying the power. In solving for problems like these, It is very important that we have a correct Thevenin/Norton equivalent circuit because if Vth and Rth is wrong, then the power dissipated by the load resistance (RL) will also be wrong.

Video(s):

Video that will explain more about the derivation in the procedure

Maximum Power Transfer

“Every idea is in the soul of its owner. No other power can shift it to another soul, that is why we have the telephone, aircraft, etc, each having its unique inventor.”
― Michael Bassey Johnson

Week 11: Thevenin's Theorem with Dependent Sources

Thevenin's Theorem with Dependent Sources

Cases in Thevenin's Theorem:

■ CASE 1: If the network has no dependent sources, we turn off all independent sources. R_TH is the input resistance of the network looking between terminals A and B. 

■ CASE 2: If the network has dependent sources, we turn off all independent sources. As with superposition, dependent sources are not to be turned off because they are controlled by circuit variables. We apply a voltage source at terminals A and B and determine the resulting current I_o. Then, R_TH = V_o/I_o . Alternatively, we may insert a current source I_o at terminals A-B and find the terminal voltage V_o. Again R_TH = V_o/I_o. Either of the two approaches will give the same result. In either approach we may assume any value of and V_o and I_o. For example, we may use V_o = 1V or I_o = 1A or even use unspecified values of V_o or I_o.

It often occurs that R_TH takes a negative value. In this case, the negative resistance (V = -iR) implies that the circuit is supplying power. This is possible in a circuit with dependent sources.

Thevenin’s theorem is very important in circuit analysis. It helps simplify a circuit. A large circuit may be replaced by a single independent voltage source and a single resistor. This replacement technique is a powerful tool in circuit design.

As mentioned earlier, a linear circuit with a variable load can be replaced by the Thevenin equivalent, exclusive of the load. The equivalent network behaves the same way externally as the original circuit. Consider a linear circuit terminated by a load R_L, . The current I_L through the load and the voltage V_L across the load are easily determined once the Thevenin equivalent of the circuit at the load’s terminals is obtained.

Suppose that R₁ =5Ω , R₂ =3Ω and I_S =2A .

Solution

The circuit has both independent and dependent sources. In these cases, we need to find the open circuit voltage to determine the Thevenin Equivalent Circuit

Open Circuit Voltage

Open circuit voltage means the voltage across the terminals of the network without connecting any extra element or connection:

Since there is no connection, the current of R₂ is zero. To solve the circuit lets write KVL for the left hand side loop assuming I_R1 defined from left to right:

+V_x+R₁×I_R1+V_x=0
→2V_x=−R₁×I_R1
→V_x=−R₁×I_R12
But what is I_R1? R₁ is in series with the current source; they have only one node shared and there is no other element connected there. This means that all current of I_S must pass through R₁ . Therefore, I_R1=I_S=2A .
If we apply this to the equation above, we have

V_x=−R₁×I_R12→V_x=−5V.
Since no current passing through R₂ we can easily see that V_OC=V_x . If it is not clear, you could find this by applying KVL to the right hand side loop:
−V_x+R₂×I_R2+V_OC=0
→−V_x+R₂×0+V_OC=0
→V_OC=V_x=−5V

Calculating R_TH

The only thing left is to calculate R_Th which can be easily found by
R­_TH=V_OC / I_SC=−5−53=3Ω

Thevenin's Equivalent Network

V_Th=V_OC=−5V
R_Th=3Ω 

Reflection/Learnings:

This week, We discussed about Thevenin's Theorem with Dependent Sources. I didnt include this in the previous section because I wanted to explain it in more detail. Actually, In Thevenin's Theorem, There were two cases. Case 1 are for circuits that doesn't have any dependent sources while Case 2 are for circuits that contains at least one dependent source. To solve for problems with dependent sources, We first turn off all independent sources by replacing all voltage sources as a closed branch and replacing all current sources with an open branch. Dependent sources cannot be turned off because they are controlled by circuit variables and then we simply remove one load in a circuit and instead of replacing it with an open circuit and measuring the open circuit voltage, We add an additional voltage or current source. The values of the added sources completely depends on you. You can assume any value for it as long as it is not 0. 

Video(s):

Thevenin's Theorem with Dependent Source

Thevenin's Theorem with one Dependent Source 

Electricity is often called wonderful, beautiful; but it is so only in common with the other forces of nature. The beauty of electricity or of any other force is not that the power is mysterious, and unexpected, touching every sense at unawares in turn, but that it is under law, and that the taught intellect can even govern it largely. The human mind is placed above, and not beneath it, and it is in such a point of view that the mental education afforded by science is rendered super-eminent in dignity, in practical application and utility; for by enabling the mind to apply the natural power through law, it conveys the gifts of God to man.

--Michael Faraday

Week 10: Thevenin and Norton's Theorem

Thevenin's Theorem

What is Thevenin's Theorem?

-Thevenin's Theorem states that it is possible to simplify any linear circuit, no matter how complex, to an equivalent circuit with just a single voltage source and series resistance connected to a load. The qualification of “linear” is identical to that found in the Superposition Theorem, where all the underlying equations must be linear (no exponents or roots). If we're dealing with passive components (such as resistors, and later, inductors and capacitors), this is true. However, there are some components (especially certain gas-discharge and semiconductor components) which are nonlinear: that is, their opposition to current changes with voltage and/or current. As such, we would call circuits containing these types of components, nonlinear circuits.

Thevenin's Theorem is especially useful in analyzing power systems and other circuits where one particular resistor in the circuit (called the “load” resistor) is subject to change, and re-calculation of the circuit is necessary with each trial value of load resistance, to determine voltage across it and current through it.

Simple Steps to Analyze Electric Circuit through Thevenin’s theorem.

* Open the load resistor

* Calculate / measure the Open Circuit Voltage. This is the Thevenin Voltage (V_TH)

* Open Current Sources and Short Voltage Sources.

* Calculate /measure the Open Circuit Resistance. This is the Thevenin Resistance (R_TH)

* Now, Redraw the circuit with measured open circuit Voltage (V_TH) in Step (2) as voltage Source and measured open circuit resistance (R_TH) in step (4) as a series resistance and connect the load resistor which we had removed in Step (1). This is the Equivalent Thevenin Circuit of that Linear Electric Network or Complex circuit which had to be simplified and analyzed. You have done.

* Now find the Total current flowing through Load resistor by using the Ohm’s Law IT = V_TH/ (R_TH + R_L)

Example:

Find V_TH, R_THand the load current flowing through and load voltage across the load resistor in fig (1) by using Thevenin’s Theorem.

Solution:

* Step 1

Open the 5kΩ load resistor (Fig 2)

Step 2

Calculate / measure the Open Circuit Voltage. This is the Thevenin Voltage (V_TH). Fig (3)

We have already removed the load resistor from figure 1, so the circuit became an open circuit as shown in fig 2. Now we have to calculate the Thevenin’s Voltage. Since 3mA Current flows in both 12kΩ and 4kΩ resistors as this is a series circuit because current will not flow in the 8kΩ resistor as it is open.

So 12V (3mA  x 4kΩ) will appear across the 4kΩ resistor. We also know that current is not flowing through the 8kΩ resistor as it is open circuit, but the 8kΩ resistor is in parallel with 4k resistor. So the same voltage (i.e. 12V) will appear across the 8kΩ resistor as 4kΩ resistor. Therefore 12V will appear across the AB terminals. So,

V_TH = 12V 

Step 3

Open Current Sources and Short Voltage Sources. Fig (4)

Step 4

Calculate /measure the Open Circuit Resistance. This is the Thevenin Resistance (R_TH)

We have Reduced the 48V DC source to zero is equivalent to replace it with a short in step (3), as shown in figure ()  We can see that 8kΩ resistor is in series with a parallel connection of 4kΩ resistor and  12k Ω resistor. i.e.:

8kΩ + (4k Ω || 12kΩ) ….. (|| = in parallel with)

R_TH = 8kΩ + [(4kΩ x 12kΩ) / (4kΩ + 12kΩ)]

R_TH = 8kΩ + 3kΩ

R_TH = 11kΩ

Step 5

Connect the R_THin series with Voltage Source V_TH and re-connect the load resistor. This is shown in fig (6) i.e. Thevenin circuit with load resistor.

Step 6

Now apply the last step i.e. calculate the total load current & load voltage as shown in fig 6.

I_L = V_TH/ (R_TH + R_L)

= 12V / (11kΩ + 5kΩ) → = 12/16kΩ

I_L= 0.75mA

And

V_L = I_Lx R_L

V_L = 0.75mA x 5kΩ

V_L= 3.75V

Norton's Theorem

What is Norton's Theorem?

-Norton's Theorem states that it is possible to simplify any linear circuit, no matter how complex, to an equivalent circuit with just a single current source and parallel resistance connected to a load. Just as with Thevenin's Theorem, the qualification of “linear” is identical to that found in the Superposition Theorem: all underlying equations must be linear (no exponents or roots).

Contrasting our original example circuit against the Norton equivalent: it looks something like this:

. . . after Norton conversion . . .

Steps to follow for Norton's Theorem:

• (1) Find the Norton source current by removing the load resistor from the original circuit and calculating current through a short (wire) jumping across the open connection points where the load resistor used to be.
• (2) Find the Norton resistance by removing all power sources in the original circuit (voltage sources shorted and current sources open) and calculating total resistance between the open connection points.
• (3) Draw the Norton equivalent circuit, with the Norton current source in parallel with the Norton resistance. The load resistor re-attaches between the two open points of the equivalent circuit.
• (4) Analyze voltage and current for the load resistor following the rules for parallel circuits.

Reflection/Learnings:

Thevenin's Theorem pretty much  simplifies an entire circuit no matter how complex into an equivalent circuit with only one Voltage source (Vth). In Thevenin's theorem, We also change one resistor into an open circuit.  It does this because we need to measure the open circuit voltage of the circuit. In Norton's theorem the same concept is pretty much applied but instead of turning one load into an open circuit and measuring the open circuit voltage, We turn it into a short circuit and then we measure the short circuit current. In this section however, I have only discussed the case 1 of Thevenin's Equivalent and in the next section, I will discuss the case 2 of Thevenin's Equivalent as well as explain both cases.

Video:

Introduction to Thevenin's Theorem

Introduction to Norton's Theorem

Engineering problems are under-defined, there are many solutions, good, bad and indifferent. The art is to arrive at a good solution. This is a creative activity, involving imagination, intuition and deliberate choice.

--Ove Arup

Week 9: Superposition

Superposition

What is Superposition?

- Superposition is another algorithmic circuit analysis method, with a prescribed procedure, like the node-voltage or loop-current methods.

It applies only in circuits with 2 or more independent sources.

It comes from the mathematical notion of superposition in which a final solution can be built as the sum of two or more partial solutions. It works well when the partial solutions can be obtained very easily. (Using voltage dividers or resistor reduction techniques.)

Superposition only applies to linear circuits, which are made up of linear circuit elements: resistors, voltage and current sources, capacitors, inductors, and linear amplifiers. It does not apply when the circuit has non-linear elements like diodes and transistors (electronics).

The Superposition Procedure:

Here are the steps: (Recall that the method only applies to circuits with two or more independent sources.)

1. Make a partial circuit by choosing one source to keep and turning of all of the other independent sources.

 -To “turn off” a voltage source, we turn it into a short circuit (zero volts and carries any amount of current.) To turn off a current source, we convert it to an open circuit (zero amps and any amount of voltage across it.)

2. Solve this “partial circuit” for the quantities of interest. Use whatever techniques that are applicable to the partial circuit: resistor reductions, voltage dividers, source transformations, or even node voltage.

3. Go back to the original circuit and create another partial circuit by choosing another source to keep (different than the first one) and turning off all of the other sources in the circuit.

4. Solve the second partial circuit for the quantities of interest.

5. Repeat the process until each independent source has been used in a partial circuit.

6. Sum up the all of the partial results to get the total results for the quantities of interest.

 -If there are n independent sources in a circuit, then when using superposition, you would expect to solve n partial circuits and find n partial results for whatever you are looking for.

Example:

4Ω and 2Ω are in series and also 3Ω and 1Ω :

Now 4Ω and 6Ω are parallel:

4Ω||6Ω=4×6/4+6=2.4Ω

So using Ohm's law:

Ix1=5V/2.4Ω=2.083A

For a moment forget Ix and concentrate on finding current of resistors. If we have the current of resistors, we can easily apply KCL and find Ix2 . So, 4Ω and 2Ω are parallel and also 3Ω and 1Ω are parallel:

4Ω||2Ω=4×2/4+2=43Ω

3Ω||1Ω=3×1/3+1=34Ω

Now, we can find their voltage drops:

V4Ω||2Ω=4/3×−3A=−4V

V3Ω||1Ω=3/4×−3A=−2.25V

Please note that the voltage drop on 4Ω||2Ω is the same as 4Ω and 2Ω voltage drops, because the circuits are equivalent and all are connected to the same nodes. The same statement is correct for 3Ω||1Ω voltage drop and 3Ω and 1Ω voltage drops. So

V4Ω=V2Ω=V4Ω||2Ω=−4V

V3Ω=V1Ω=V3Ω||1Ω=−2.25V

To find Ix2 all we need is to write KCL at one of the nodes:

−I2Ω+Ix2+I3Ω=0

→Ix2=I2Ω−I3Ω 

I2Ω and I3Ω can be found using Ohm's law:

I2Ω=V2Ω2Ω=−42=−2V

I3Ω=V3Ω3Ω=−2.253=−0.75V

Therefore,

Ix2=−1.25A

And

Ix=Ix1+Ix2=2.083−1.25=0.8333A

Ix=0.8333A

Reflection:

Superpositon overall is a topic with an easy-to grasp concept. To solve a circuit using the superposition theorem, We need to choose one source and then we need to turn off the other sources. The choosing of the sources is the most crucial part because choosing the wrong source to turn on might lead to a wrong output. After that, its only a matter of applying the basic circuit laws and equations to solve the problem.

Video:

Superposition

Superposition problem with dependent source

Thanks for visiting my Blog!!. The tenth post wont be arriving for a while. See ya!!!

I find that the harder I work, the more luck I seem to have.

-Thomas Jefferson